Le problème des généraux byzantins

Le problème des généraux byzantins est un problème d'informatique distribuée qui a été formalisé par Leslie Lamport, Robert Shostak et Marshall Pease en 1982. Il s'agit d'une métaphore faisant intervenir des généraux qui assiègent une ville ennemie et désirent l'attaquer avec leur armée. Le problème a été remis au goût du jour suite au succès de Bitcoin, inventé en 2008 par Satoshi Nakamoto, qui y apportait une solution originale.

Dans la métaphore, l'armée est celle de l'Empire Byzantin, aussi connu comme l'Empire romain d'Orient, qui a perduré jusqu'en 1453 après sa séparation avec l'Empire d'Occident en 395, et qui s'étendait aux alentours de la Grèce et de la Turquie. Le nom de cet empire fait référence à « Byzance », le nom antique de sa capitale, renommée Constantinople par Constantin I^er, et qui est aujourd'hui appelée Istanbul.

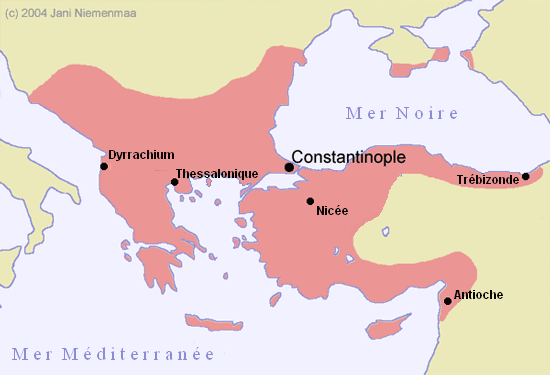
D'après Leslie Lamport lui-même, les généraux devaient originellement être albanais mais il en a été décidé autrement. Dans le problème, l'armée comporte des traîtres. Il fallait donc choisir une nationalité qui ne risque pas d'offenser le sentiment patriotique du lecteur. L'Albanie, qui était un pays très fermé à l'époque, constituait un choix acceptable. Cependant, l'option byzantine était bien meilleure, car « byzantin » constituait une appellation a posteriori à laquelle personne ne s'identifiait profondément.

Le problème

Le problème des généraux byzantins est plutôt simple à énoncer. Des généraux de l'armée byzantine campent autour d'une cité ennemie avec leurs unités et souhaitent l'attaquer. Ils ne peuvent communiquer qu'à l'aide de messagers oraux et doivent établir un plan de bataille commun. L'idée est de coordonner une attaque à un moment précis, disons à l'aube. Les généraux partagent ce qu'ils vont faire en envoyant le message « attaque » pour confirmer l'assaut, et « retraite » pour l'annuler.

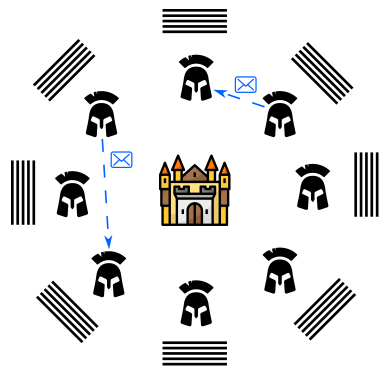
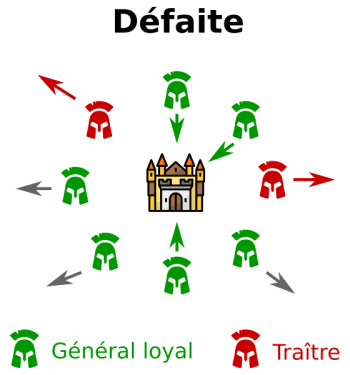
Cependant, un certain nombre de ces généraux peuvent s'avérer être des traîtres qui essaient de semer la confusion au sein de l'armée. Ainsi, ils envoient le message « retraite », pour convaincre certains généraux loyaux de battre en retraite au moment de l'assaut et pour causer une défaite certaine.

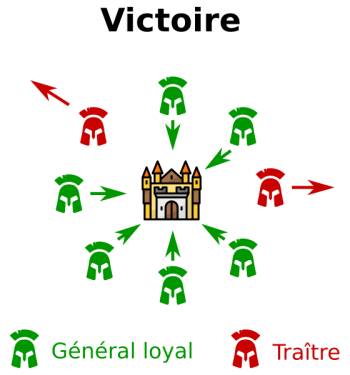
Le problème est de trouver une stratégie (c'est-à-dire un algorithme) pour s'assurer que tous les généraux loyaux arrivent à se mettre d'accord sur un plan de bataille. Les traîtres trahiront tout de même en battant en retraite, mais puisque leur nombre est supposé être restreint, l'attaque sera un succès.

Même en désignant des commandants auxquels des généraux subordonnés obéiront, la situation fait qu'il est très difficile de parvenir à un consensus car le commandant peut également être un traître.

Pourquoi ce problème est-il important ?

La situation très imagée des généraux byzantins peut se rencontrer dans des systèmes informatiques divers qui nécessitent une certaine synchronisation. Elle est notamment problématique dans des domaines critiques, comme l'aéronautique : l'infrastructure informatique du Boeing 777 prend par exemple en compte les pannes byzantines.

Mais ce problème se rencontre surtout au sein des réseaux pair-à-pair de nœuds souhaitant se mettre d'accord sur le contenu d'un registre. Bitcoin par exemple se base sur un réseau de participants qui entretiennent chacun le registre des transactions réalisées : la fameuse chaîne de blocs.

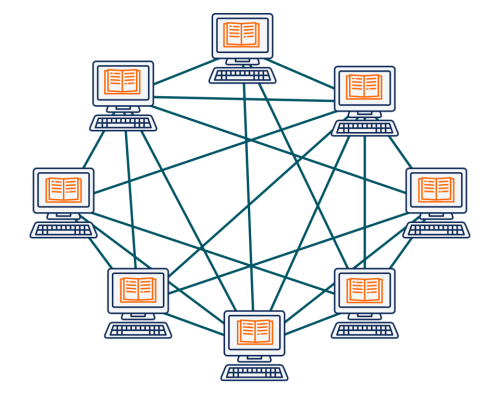
Ces systèmes sont en effet soumis aux pannes byzantines (byzantine faults), représentées par les messages des traîtres dans le problème des généraux byzantins. Le but est donc de trouver un algorithme qui permettrait à tous les nœuds honnêtes de se mettre d'accord en présence de nœuds traîtres (ou « byzantins »), c'est-à-dire parvenir à un consensus. La propriété possédée par ce type d'algorithme s'appelle la tolérance aux pannes byzantines, ou byzantine fault tolerance en anglais, qui est souvent abrégée en BFT.

Dans le cas de Bitcoin qui est un système de transfert de valeur, l'enjeu est de se mettre d'accord sur qui possède quoi de manière distribuée, sans reposer sur une autorité centrale comme cela est fait dans le système bancaire, et sans que des nœuds malveillants ne puissent altérer le consensus.

Comment c'est résolu ?

Il a été montré que le problème des généraux byzantins peut être résolu de manière absolue si (et seulement si) les généraux loyaux représentent strictement plus des deux tiers de l'ensemble des généraux. Autrement dit, il ne peut pas y avoir plus d'un tiers de traîtres au sein de l'armée.

Avant Bitcoin, le problème était ainsi résolu par des algorithmes dits « traditionnels » qui étaient soumis à des contraintes fortes, notamment sur le nombre de nœuds pouvant interagir. Le plus connu est sans doute l'algorithme de consensus PBFT (pour Practical Byzantine Fault Tolerance), qui a été mis au point par Miguel Castro et Barbara Liskov en 1999. Il permet à un nombre donné de participants de se mettre d'accord en gérant des milliers de requêtes par seconde avec une latence de moins d'une milliseconde. Des variantes de PBFT sont encore utilisées aujourd'hui au sein de protocoles gérant des registres distribués comme Hyperledger Sawtooth (Sawtooth PBFT) et Neo (dBFT). Il existe également bien d'autres algorithmes traditionnels qui se basent sur les mêmes idées et ont les mêmes propriétés.

Ces systèmes souffrent néanmoins d'un défaut majeur : ils ne sont pas très robustes. Il faut sélectionner préalablement les nœuds ayant le droit de participer au consensus : cela peut se faire par preuve d'autorité (proof-of-authority), via une liste blanche de nœuds, ou par preuve d'enjeu déléguée comme c'est fait dans Neo. Dans les deux cas, le système est relativement fermé et vulnérable aux attaques extérieures, puisque les nœuds validateurs sont connus de tous et donc soumis aux aléas de la réalité.

Avec l'invention de Bitcoin en 2008, c'est un nouvel algorithme de consensus qui apparaît : l'algorithme de consensus de Nakamoto par preuve de travail. Celui-ci met en jeu des blocs de transactions, qui sont ajoutés à une chaîne par le biais d'une dépense d'énergie électrique (d'où le terme de preuve de travail), et c'est la chaîne qui accumule le plus d'énergie (« la chaîne la plus longue ») qui est considérée valide. S'il peut y avoir des divergences ponctuelles dans le consensus (embranchements), ce n'est très souvent pas le cas en raison des incitations économiques du protocole : les validateurs, appelés mineurs, utilisent leur puissance de calcul en l'échange d'une récompense en bitcoins, et n'ont pas de réel intérêt à œuvrer contre le bon fonctionnement du système.

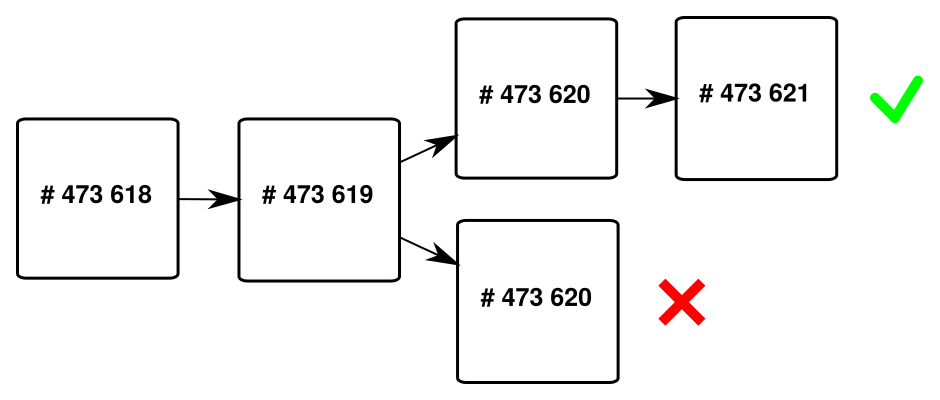
Embranchement de la chaîne de blocs — *Embranchement (fork) bénin de la chaîne : la chaîne valide est la plus longue.*

L'idée géniale derrière Bitcoin a été de résoudre le problème des généraux byzantins de manière probabilistique, plutôt que de manière absolue. En effet, dans les algorithmes traditionnels, une finalité est atteinte ; dans Bitcoin ce n'est jamais le cas, mais il est possible d'estimer qu'une transaction est irréversible après qu'un certain nombre de blocs aient été minés. De plus, l'algorithme de Nakamoto ne se repose pas sur l'hypothèse très contraignante des 67 % de nœuds honnêtes : avec Bitcoin, seule la moitié de la puissance de calcul doit être honnête.

Ainsi, contrairement aux algorithmes traditionnels, l'algorithme de Nakamoto permet à un très grand nombre de nœuds de participer de manière totalement ouverte sans que son fonctionnement en pâtisse. Cela est très important pour un cas d'usage aussi sensible que la monnaie, car il s'agit, rappelons-le, d'une fonction économique soumise à un monopole à peu près partout sur le globe, et toute tentative de concurrence ne saurait rester impunie aux yeux de l'État. Bitcoin doit exister en dehors des lois s'il veut exister tout court. Et c'est aussi pour cette raison que la libra ne verra peut-être jamais le jour : Libra est en effet basé sur un algorithme traditionnel du nom de LibraBFT impliquant une centaine de validateurs, ce qui amoindrit sa capacité à résister à la censure et à exister de manière indépendante des États.